General guidance
Concepts and reason
The concepts related to solve this problem are momentum, kinetic energy and mechanical energy.
Fundamentals
The momentum of a body is defined as the product of mass and velocity. The expression is given as follows:
Here, m is the mass and v is the velocity.
The gravitational potential energy of a body is given as follows:
Here, g is the acceleration due tom gravity, h is the height and m is the mass.
The kinetic energy of a body is given as follows:
The mechanical energy of the body is defined as the sum of kinetic energy and potential energy. The expression is given as follows:
Step-by-step
Step 1 of 5
When the baseball is thrown vertically upwards, the force of gravity acting on the ball changes its velocity. As the velocity of the ball changes, the momentum and kinetic energy of the ball changes.
Hence, there is no conservation of kinetic energy and momentum.
As the baseball is moving upwards, the force of gravity acts downwards resulting in decrease of the velocity and height increases resulting in increase in the gravitational potential energy.
Because of the change in velocity the kinetic energy and momentum is not conserved.
Do not consider that the momentum is conserved because it depends on the velocity and velocity changes as ball is moving upwards.
Find out how the momentum and kinetic energy changes as baseball are thrown vertically upwards.
Step 2 of 5
When the baseball is thrown vertically upwards, the force of gravity acting on the ball changes its velocity. As the velocity of the ball changes, the momentum and kinetic energy of the ball changes.
Hence, there is no conservation of kinetic energy and momentum.
As the baseball is moving upwards, the force of gravity acts downwards resulting in decrease of the velocity and height increases resulting in increase in the gravitational potential energy.
Because of the change in velocity both the kinetic energy and momentum is not conserved.
Find out how the momentum and mechanical energy changes as baseball are thrown vertically upwards.
Step 3 of 5
When the baseball is thrown vertically upwards, the force of gravity acting on the ball changes its velocity. As the velocity of the ball changes, the momentum and kinetic energy of the ball is also changes.
Hence, momentum is not conserved.
The mechanical energy of the system is given as follows:
As the ball is moving upwards, its kinetic energy decreases as the velocity of the ball decreases but the gravitational potential energy increases with the same amount. Hence, both the factors balance each other resulting in conservation of mechanical energy.
Hence, only the mechanical energy is conserved.
The mechanical energy is the sum of potential and kinetic energy. When the ball is thrown upwards, kinetic energy decreases but potential energy increases with the same amount. Hence, only the mechanical energy of the system remains conserved not momentum or kinetic energy.
Find out how the momentum and gravitational energy changes as baseball are thrown vertically upwards.
Step 4 of 5
The gravitational potential energy depends on the height which also changes as ball moves up. Therefore, the gravitational potential energy is also not conserved.
When the baseball is thrown vertically upwards, the force of gravity acting on the ball changes its velocity. As the velocity of the ball changes, the momentum and kinetic energy of the ball is also changes.
Hence, momentum is not conserved.
As the baseball is moving upwards, the force of gravity acts downwards resulting in decrease of the velocity and height increases resulting in increase in the gravitational potential energy.
Due to the two factors, the gravitational potential energy and momentum is not conserved.
Find out how the momentum and mechanical energy changes as baseball are thrown vertically upwards.
Step 5 of 5
When the baseball is thrown vertically upwards, the force of gravity acting on the ball changes its velocity. As the velocity of the ball changes, the momentum and kinetic energy of the ball changes.
Hence, momentum is not conserved.
The mechanical energy of the system is given as follows:
As the ball is moving upwards, its kinetic energy decreases as the velocity of the ball decreases but the gravitational potential energy increases with the same amount. Hence, both the factors balance each other resulting in conservation of mechanical energy.
Hence, the mechanical energy is conserved.
Its momentum is not conserved, but its mechanical energy is conserved.
Mechanical energy is defined as the energy associated with position and motion of an object.
Answer
Its momentum is not conserved, but its mechanical energy is conserved.
Answer only
Its momentum is not conserved, but its mechanical energy is conserved.
р-ту
PE mgh
KE=mv 2
= KE+ PE TE 1 -mv +mgh 2
1 ME=mvmgh МЕ 2
1 ME=mvmgh МЕ 2
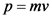
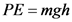
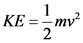
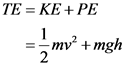
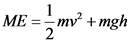
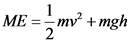
- Purchase Order Templates - April 26, 2024
- Windows 8.1 Media Center Pack - April 26, 2024
- Statement: The new xbox series x overheats and shutsdown with normal use. Microsoft please address this issue - April 26, 2024
