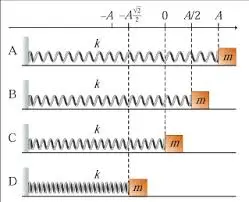
Figure 1 shows a harmonic oscillator at four different moments,
labeled A, B, C, and D. Assume that the force constant k, the mass
of the block, m, and the amplitude of vibrations, A, are given. We
will also assume that there are no resistive forces so the total
energy of the oscillator remains constant. In part (d) to part (h),
when asked “which moment”, you can indicate the answer by the
letter A, B, C, or D. (a) What is the total energy energy of the
system? (b) What is the maximum potential energy of the system? (c)
Find the kinetic energy of the block at the moment labeled B. (d)
Which moment corresponds to the maximum potential energy of the
system? (e) Which moment corresponds to the minimum potential
energy of the system? (f) Which moment corresponds to the maximum
kinetic energy of the system? (g) Which moment corresponds to the
minimum kinetic energy of the system? (h) At which moment is KE = P
E? Explain mathematically. No points will be given for part (h) if
you do not explain your logics.
The total energv is equal to -kA Here, K is the force constant and A is the amplitude. At A, there is no velocity and hence, there is no kinetic energy The maximum potential energy is when the kinetic energy is zero. The kinetic energy is zero where the velocity is zero, and the velocity is zero at point A
At point B, The total potential energy is, Apply the law of conservation of energy as follows 322 3 k 2 Thus, the velocity at point B is, Thus, the kinetic energy is, The moment where the kinetic energy is equal to zero is the point of maximum expansion The kinetic energy is zero at point A The moment the particle is at point A corresponds to the maximum potential energy of the systenm
- Unshare workbook is greyed out Excel 2016?? - April 18, 2024
- Something went wrong, and Outlook couldn’t set up your account , but the problem persists - April 18, 2024
- how do I save clip art as picture? - April 18, 2024
