The following functions are undefined at x = 0. For each,
determine if this point of discontinuity is removable, and if so,
state the value for the function at 0 that allows for the
continuous extension. a) i(x) =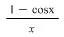 
b) j(x) =
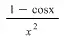
a removable discontinuity is one at which the limit of the
function exists but does not equal the value of the function at
that point; this may be because the function does not exist at that
point.
now for both the functions , the discontinuity at 0 is removable
and the value for
continuous extension is the limit of the function at that point can
be found out using L’hospital’s rule….
for i(x)= 1-cos x/x
hence if f(0) = 0 then function becomes continuous
for j(x) = 1-cosx/x^2
hence if f(0) = 1/2 function becomes continuous
a removable discontinuity is one at which the limit of the function exists but does not equal the value of the function at that point: this may be because the function does not exist at that point. now for both the functions, the discontinuity at 0 is removable and the value for continuous extension is the limit of the function at that point can be found out using L’hospital’s rule…. for i(x) = 1-cos x/x lim_x rightarrow 0 1 – cos x/x = lim_x rightarrow 0 d/dx (1 – cos x)/(d/dx x) = lim_x rightarrow 0 sin x = 0 hence if f(0) = 0 then function becomes continuous for j (x) = 1 – cos /x^2 lim_x rightarrow 0 1 – cos x/x^2 = lim_x rightarrow 0 sin x/2x = 1/2 hence if f(0) = 1/2 function becomes continuous
- what is the meaning of 3YWLO stamped on a cross neckless? - April 17, 2024
- Realtek audio driver Windows 11 - April 17, 2024
- How to stop Microsoft SharePoint pop up continually asking me to share confidential information stored in keychain - April 17, 2024
